fixed xor implementation
If you are a person who is constantly having trouble when making decisions like me, that means you use the word ‘OR’ a lot in your life.
In computer science, the ‘OR’ operator is fairly common, but probably not because computer scientists have trouble when making decisions.
And adding ‘exclusive’ to the beginning of a word always makes that word cooler. Right?
You can use this operator just because it’s super cool (I think it’s a pretty good reason). However, those dealing with cryptography have good reasons to use the ‘XOR’ operator. XOR allows you to easily encrypt and decrypt a string. You cannot do this with other logical operators:
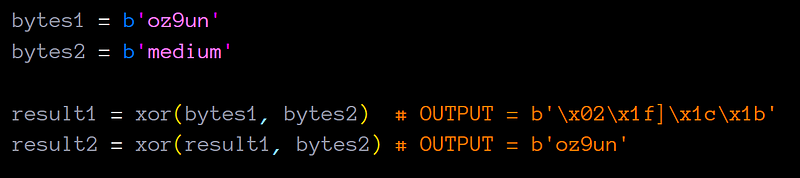
In this article, we won’t start with inserting words into the XOR operator as above. With a more basic and fun challenge, we will see how we can do the Fixed XOR operation in Python.
And the purpose here is not to solve the challenge quickly and in the shortest way, but to fully understand the processes and the functions used. Thus, to use it effectively in different questions/challenges.
Spoiler: We’ll do that as in the base64 post, without importing any modules!
WARNING: Don’t be angry with me for not explaining what XOR is from the beginning, just believe it would be boring if I explained at length that it is just the sum of two bits in mod 2.
The challenge we’ll rock:
We will solve Challenge 2 of Set 1 on the cryptopals: Fixed XOR.
Cryptopals is a very well crafted site with lots of crypto challenges. Must be visited by beginners and those who want to improve themselves!
First, let’s examine the challenge:

Challenge:
Write a function that takes two equal-length buffers and produces their XOR combination.
If your function works properly, then when you feed it the string:
1c0111001f010100061a024b53535009181c
... after hex decoding, and when XOR'd against:
686974207468652062756c6c277320657965
... should produce:
746865206b696420646f6e277420706c6179
Battle time! (or coding):

1- Converting HEX to integer:
Firstly, we need to convert hex to integer (I’ll also explain that we don’t actually need).
Python has a int() function, which takes 2 parameters:
int(α, base)
α = the number to be converted to an integer (It works with and without the 0x prefix)
base = base of the α
As we know, the “hex” system is a number system consisting of 16 symbols. That means “hex” is base 16.
Example usage of int() function to convert hex to integer:
hex_value = "CAFEBABE" # or "0xCAFEBABE"
base = 16
result = int(hex_value, base)

2- Converting integer to binary:
Python has a bin() function, which takes 1 parameter.
bin(α)
α = any numeric value
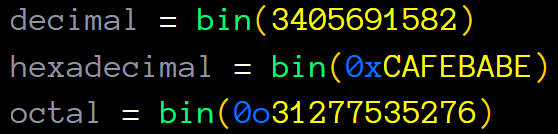
Any numeric value… That means you can:
decimal = bin(3405691582)
hexadecimal = bin(0xCAFEBABE)
octal = bin(0o31277535276)
And they all give the same “binary string” output:
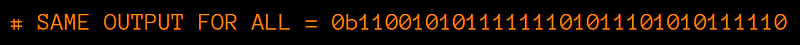
I didn’t want to spoil the originality as the ‘0x’ prefix was not given in the challenge, so I first converted it to integer. If you wish, you can add the 0x prefix and use the bin() function directly.
3- Converting binary to desired format:
What is desired format?
To get the desired format, we have to solve the following 2 problems:
- [Output of the bin() function always prefixed with ‘0b’.]
- [The bin() function always tries to express the number in the shortest way.]
What I mean is:

It will be convenient for us to have equal length of outputs to do bit by bit XOR operation. But as seen above, the length of the output depends on the value of the input.
We can solve our 1st problem by excluding the first two values of our output:

To solve 2nd problem, how can we make both outputs equal?
Python has a zfill() function, which takes 1 parameter.
zfill(width)
width = desired length of output
zfill() function basically adds 0 to the beginning of the output, bringing it to the desired length.
Therefore, we must first find out which of the two values we will XOR are long. Then we have to make the other output to that length:
# example hex values:
hex_1 = "CAFEBABE"
hex_2 = "0A0A0A0A"
bin_1 = bin(int(hex_1, 16))[2:]
bin_2 = bin(int(hex_2, 16))[2:]
# find out length of the longer binary:
desired_length = len(bin_1) if len(bin_1) > len(bin_2) else len(bin_2)
# use zfill() to make equal lengths:
bin_1 = bin_1.zfill(desired_length)
bin_2 = bin_2.zfill(desired_length)
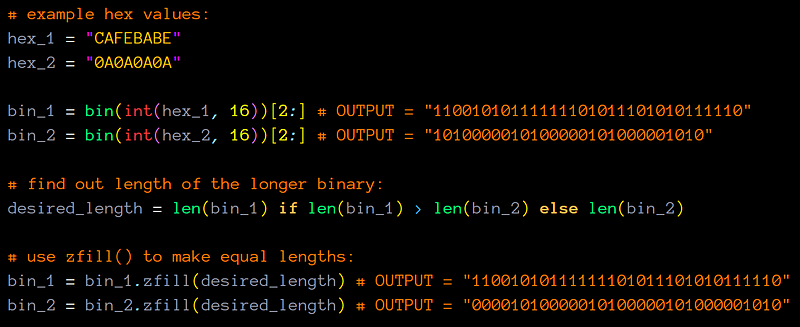
Finally, we have two binary values of the same length.
4- XOR:
We can aggregate two binary values with the zip() function and apply XOR operation bit by bit in one line:
bin_1 = "11001010111111101011101010111110"
bin_2 = "00001010000010100000101000001010"
result = [int(bit1)^int(bit2) for bit1,bit2 in zip(bin_1,bin_2)]

The only problem there is, result returns “list”:

We can easily convert this to a string value:
string_result = "".join([str(bits) for bits in result])

Now, we are ready for the last part!
5- Binary to HEX:
Python has a hex() function, which takes 1 parameter.
hex(α)
α = integer number
hex() function converts an integer number to its corresponding hexadecimal string with ‘0x’ prefix.
That’s good! But…We have binary number. Is that okay?
Yeah! At this point, we can use the int() function we learned at the beginning:
hex(int(string_result,2))

Yayyyyyy, we made it!

FINAL:

As I said before, the purpose here is not to solve the challenge quickly and in the shortest way, but to fully understand the processes and functions used. Now that we’ve revealed all the details, we can solve the real challenge:
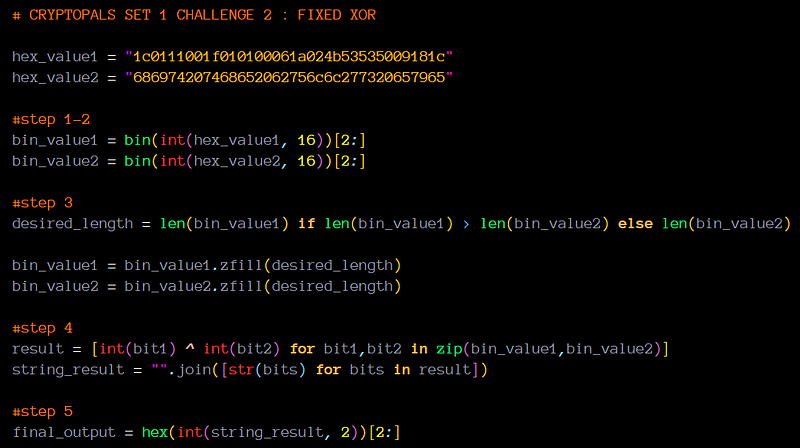
# CRYPTOPALS SET 1 CHALLENGE 2 : FIXED XOR
hex_value1 = "1c0111001f010100061a024b53535009181c"
hex_value2 = "686974207468652062756c6c277320657965"
#step 1-2
bin_value1 = bin(int(hex_value1, 16))[2:]
bin_value2 = bin(int(hex_value2, 16))[2:]
#step 3
desired_length = len(bin_value1) if len(bin_value1) > len(bin_value2) else len(bin_value2)
bin_value1 = bin_value1.zfill(desired_length)
bin_value2 = bin_value2.zfill(desired_length)
#step 4
result = [int(bit1) ^ int(bit2) for bit1,bit2 in zip(bin_value1,bin_value2)]
string_result = "".join([str(bits) for bits in result])
#step 5
final_output = hex(int(string_result, 2))[2:]
If you’ve come this far, you either really interested and enjoyed it, or you just wanted to learn the answer. Both options look pretty good, thanks!
Source code: https://github.com/oz9un/crypto_basics/blob/master/medium_writings/cryptopals12_medium.py
I’m just one email away from you for any feedback / question:
Gmail: [email protected]
Github: https://github.com/oz9un
Twitter: https://twitter.com/oz9un
By Özgün Kültekin on January 26, 2021.